Números Complejos Resumen

De números complejos cuando están puestos en forma binómica sean fáciles de recordar ya que formalmente los vamos a sumar y multiplicar como si fueran números reales y simplemente tendremos en cuenta que i2.

Números complejos resumen. La razón principal detrás de esto es que los matemáticos desarrollaron una. Matemática Aplicada y C. Cada número imaginario puede ser escrito como ib numero complejo.

Francisco Raúl Ortíz González 2008. Para cada valor de k se tiene una determinación o rama de la. Z 3 2 i.

Cuáles son los números complejos y los números reales Empezamos conociendo con detalle la definición de los números reales y complejos para que así puedas entender mejor la teoría. Si aparece i 2 reemplazar con 1. Un número imaginario es un número cuyo cuadrado es negativo.

Números complejos iguales conjugados y opuestos en las formas trigonométrica y polar. Todas estas propiedades se resumen diciendo que. APUNTES ÁLGEBRA NÚMEROS COMPLEJOS.

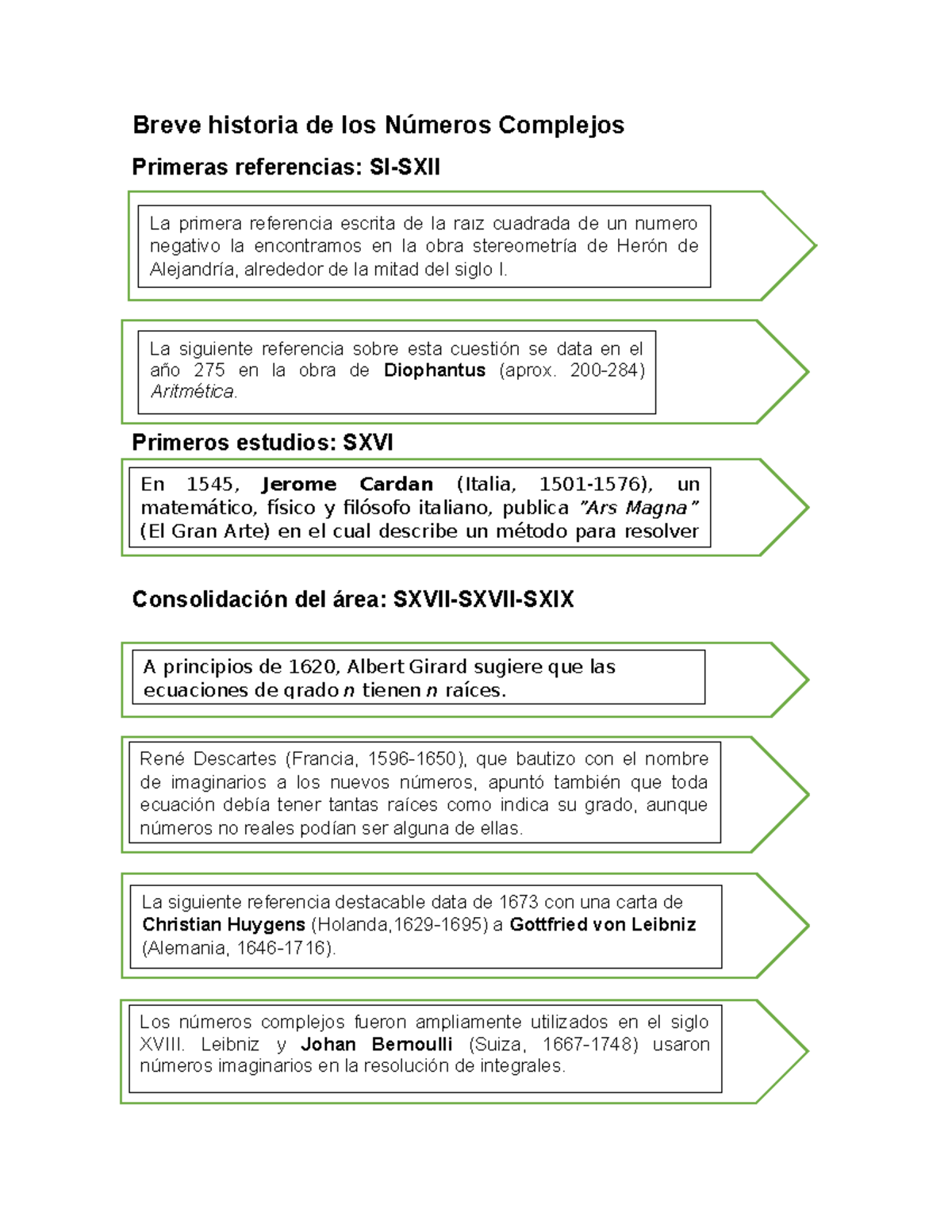
Este término fue destacado por René Descartes en el siglo XVII y expresaba claramente sus creencias. Ya comenzada la segunda mitad del siglo XIX las dudas y misterios sobre los numeros complejos ya han desaparecido aunque haya textos del siglo XX que aun huıan de utilizarlos. Números complejos 1.

Z 1 3 i. Una lista de los puntos de resumen de la lección que han estudiado los Números complejos de módulo Module 1. Build Your Free Resume in Minutes No Writing Experience Required.